Statistics
From LimeSurvey Manual
General
The purpose of a survey is to "get answers to questions". Once you have created, activated and invited participants to complete your survey, you can use the Responses & Statistics functionality to collect and analyze survey results to get answers.
The statistics feature is located under the responses menu of an active survey: Responses > Responses and Statistics Responses is only available if a survey has been activated.
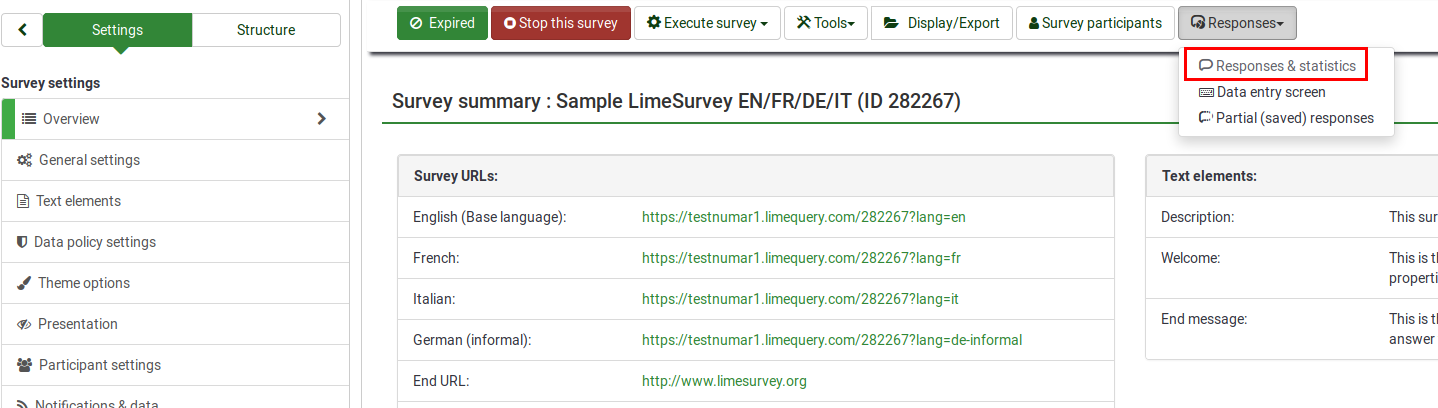
Click Statistics located on the top toolbar.

The following page will be displayed.

The LimeSurvey statistics can be displayed in either expert mode or simple mode. By default, expert mode is displayed when you click Statistics
Statistics - expert mode
Your survey is finished and you now want to start analyzing the results. LimeSurvey can export all of the results into an Excel spreadsheet or CSV file.
The statistics - expert mode feature allows you to 'filter' your data and retrieve numbers and summaries of different fields. The statistics script does not do highly complex filtering, but there is a lot of very useful information that can be easily obtained.
Running quick statistics
In the screenshot below, you can see that there is a checkbox for each question that can be selected in order to show a response summary for each question and an icon that, when clicked (or if the mouse hovers over it), gives you the full text of the question. To view the results for a question or questions, check the checkbox(es) at the top of the question(s) and then click "View statistics".
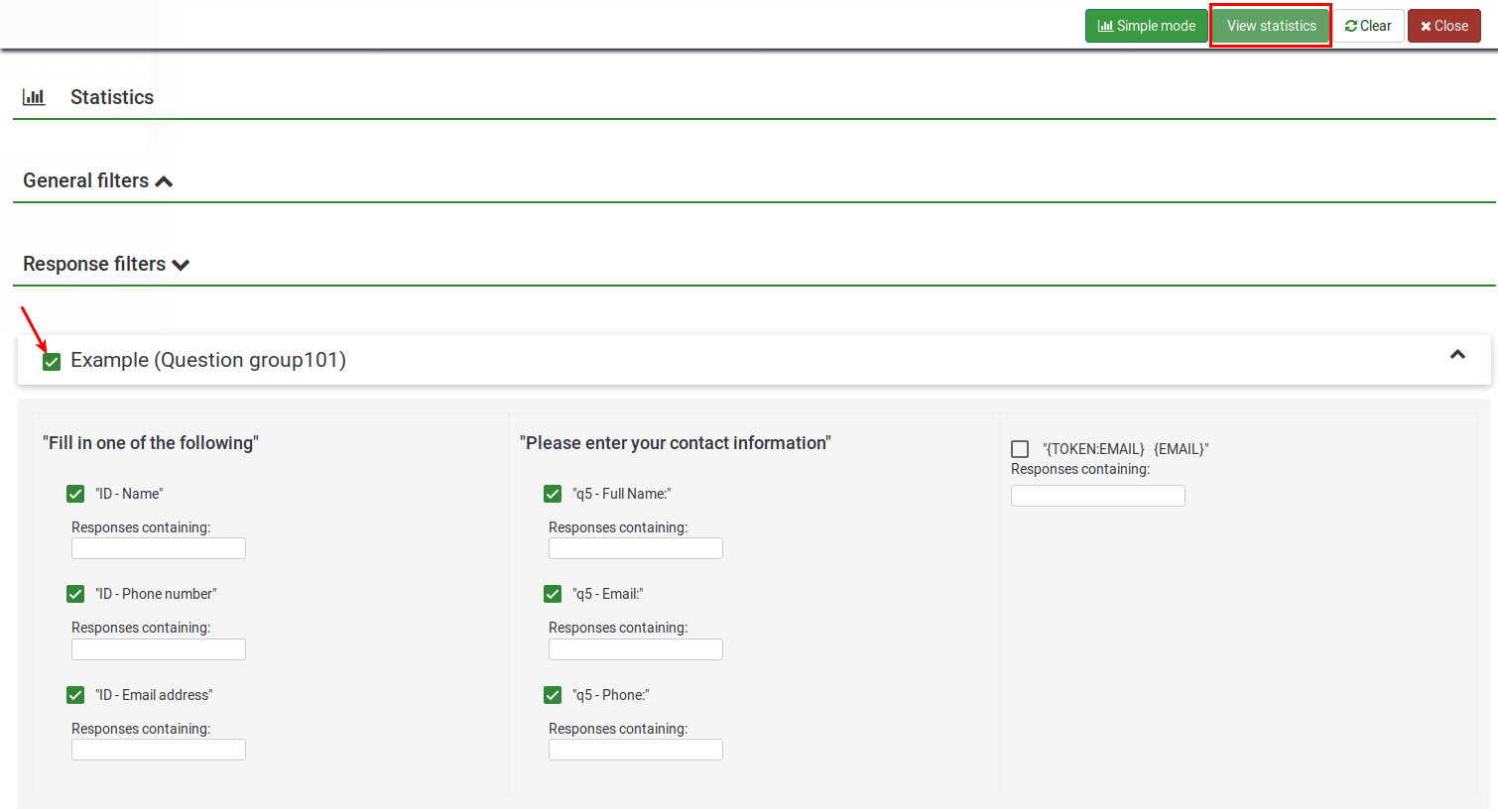
Alternatively, to view the results for all available questions, enable "View summary of all available fields" and then click "View statistics".

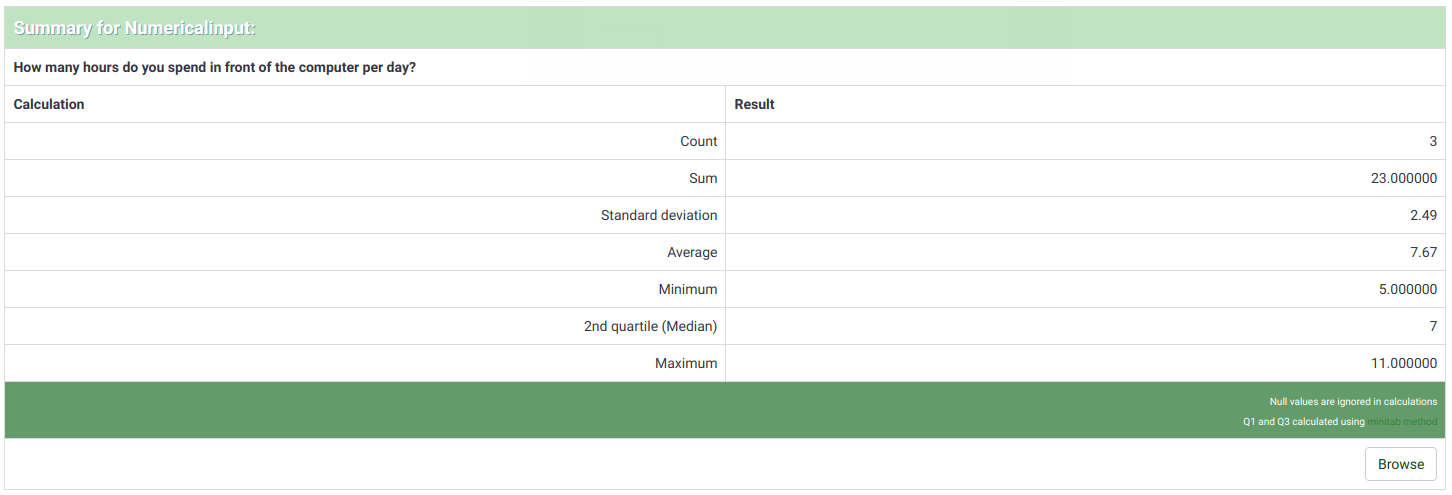
You will then be given a "Results" table which will indicate the number of cases and a "Field Summary" table for each question selected which summarizes all possible answers in the question(s), their totals, and their corresponding percentage.

Filtering data
Two types of filters exist: general and response filters.
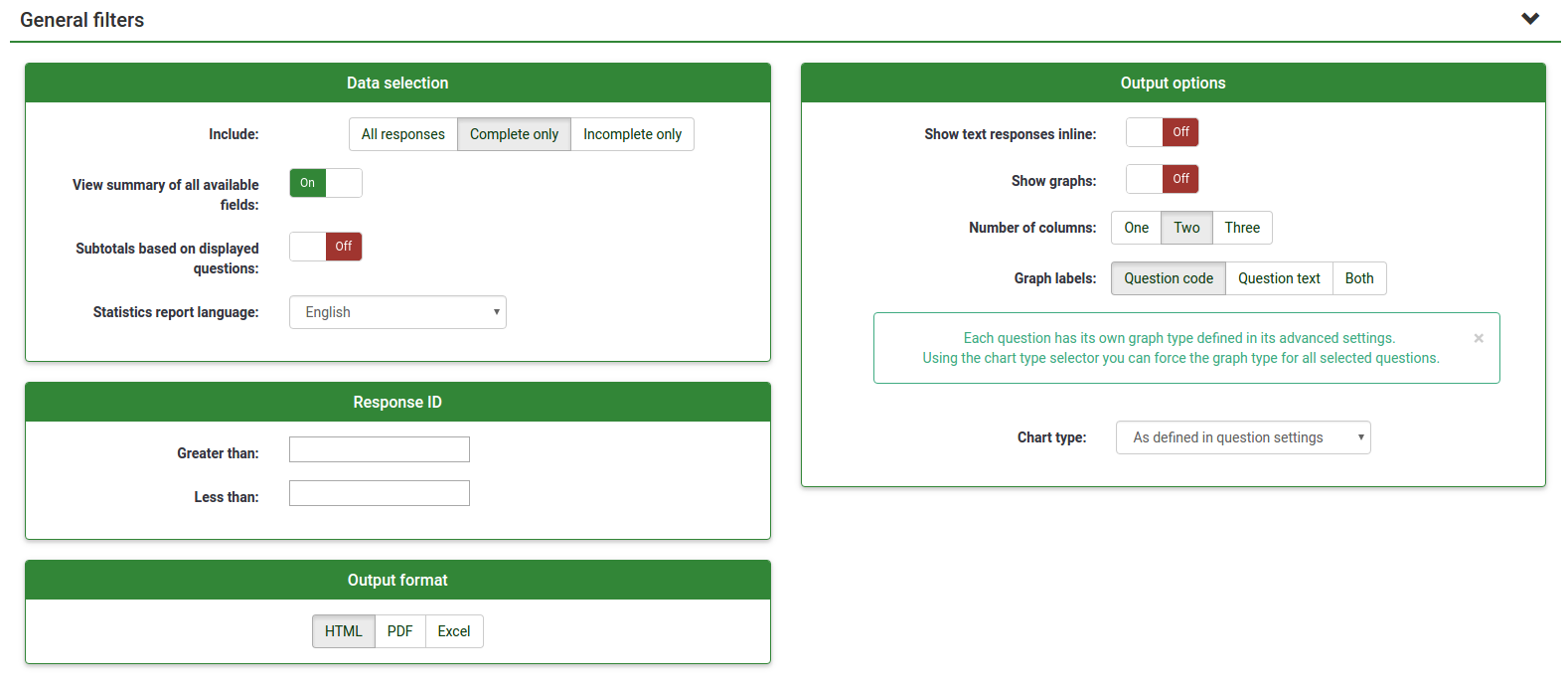
General filters
As the name suggests, General Filters refers to filters at the general (macro) level.
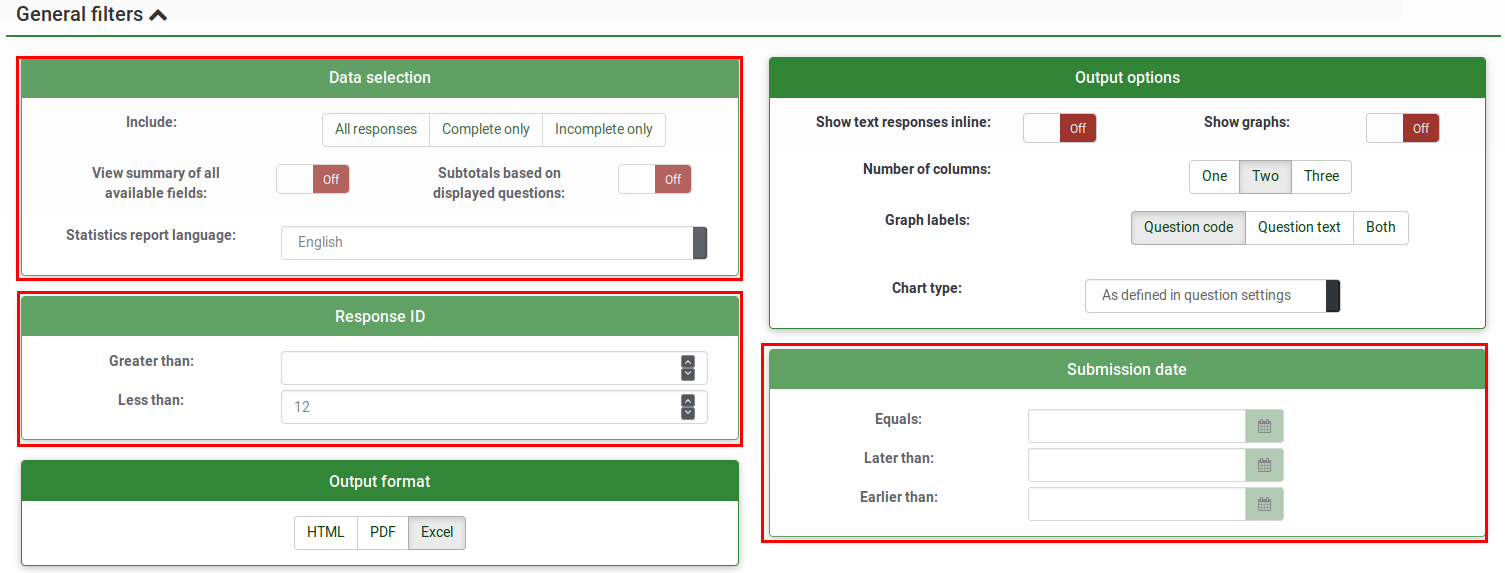
The filters can be related to:
- Data selection
- The type of responses:
- Complete responses: responses that contain a submission date
- Incomplete responses: answers that do not contain a submission date
- All records: the aggregated number of complete and incomplete responses.
- Statistics report language: if additional languages are used, this filter option is useful for dividing participants based on the language they used to fill complete the survey..
- The type of responses:
- View summary of all available field: Turned off by default. By enabling it, all the survey questions and groups will be taken into account when running the statistics script
- Subtotals based on displayed questions: Deactivated by default. It counts stats for each question based only on the total number of responses for which the question was displayed (good way to filter the unfinished/incomplete responses).
- Response ID: Use the ID number to filter your gathered responses
- Submission date:Displayed only if timings is enabled. You can filter the data based on the submission date of your collected responses.
To get the answers filtered according only to the general filters, enable the "View summary of all available field" option and click the View statistics button located in the upper-right part of the screen.
Response filters
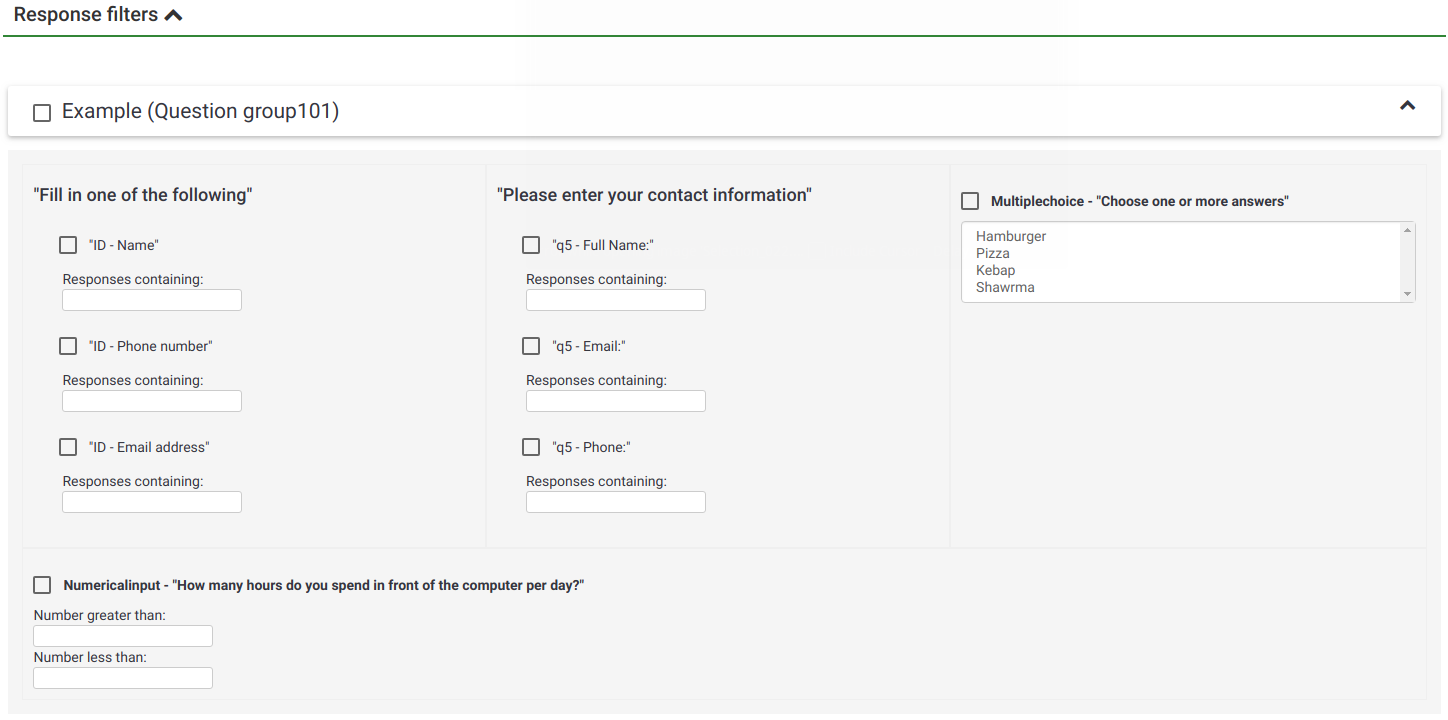
Depending on the used question type, different fields may be used to filter your answers:
- By response: Click one or more responses in the list under each question to filter the data by those responses (use CTRL/click to select multiple responses in the same question). Note that if you choose to view the summary of all available fields (checkbox at top) you will need to select your response filters before checking that box.
- By text:You can search the responses to a free text question type (and similar types) by entering a text. If you want to search for a partial string you can use the percentage sign (%) as wildcard. E.g.: If you look for 'Tom%', it will find entries with 'Tomb' and 'Tommy', etc.
- By numerical value: You can search the responses that contain a certain numerical value if number-based question types are used.
Selecting View statistics will then give you the Results table, indicating the number of responses matching your criteria, and a Field Summary table for each question selected which summarizes all possible answers in the question(s), their totals and their percentage. It is important to note that these results are a subset of your total responses. So, for example, if your criteria display 146 records out of a total 180, the summary will show the breakdown of just those 146 records for that table.
The images below indicate that the user has elected to view the stats for "Employment status" of completed records/female/age 18-25. This gives returns the results for 6 out of 13 records.
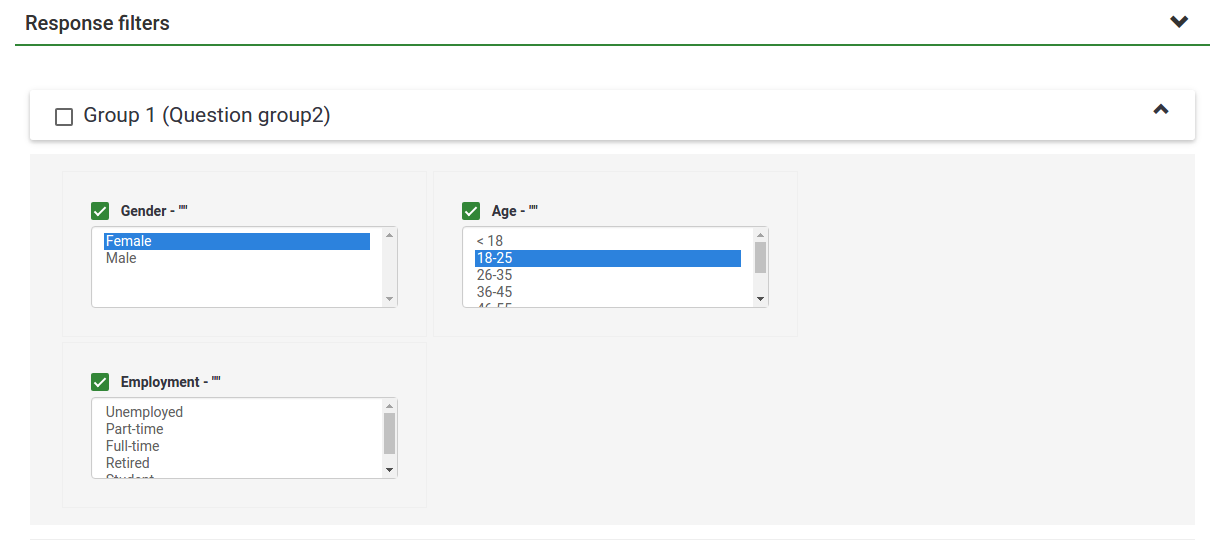
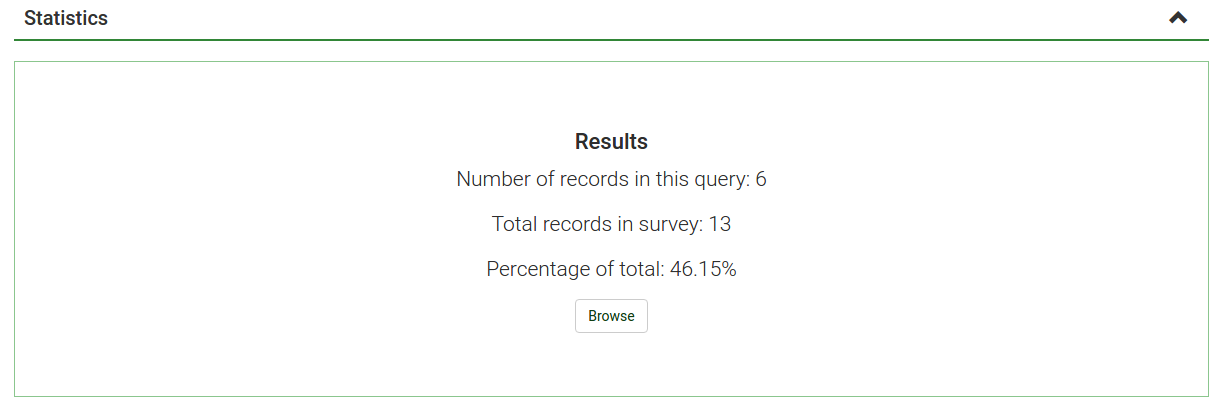
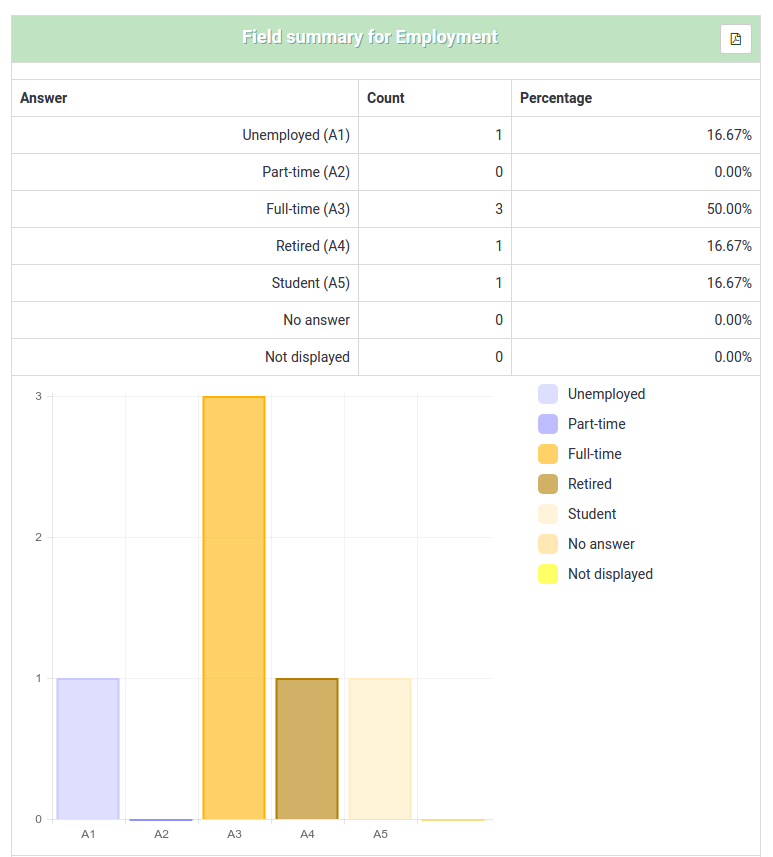
- If you set criteria on the same question that you ask for a summary, then that question will only present answers matching your criteria. So it is good practice not to set any criteria on the same question you are getting a summary of.
- To select multiple entries for a question hold down the CTRL button when clicking. To "unselect" the last criteria (if you want to clear all criteria from a question) click on the respective highlighted answer while holding pressed the CTRL button.
Graphs
For charting, the library pChart is used, which is completely included and usually doesn't have to be configured.
After the graphs have been generated you can export them easily. Right click on graph and choose "Save image as", then save the graph as a .png file to your chosen location.
You can also use the "Export images" function to save all the graphs.
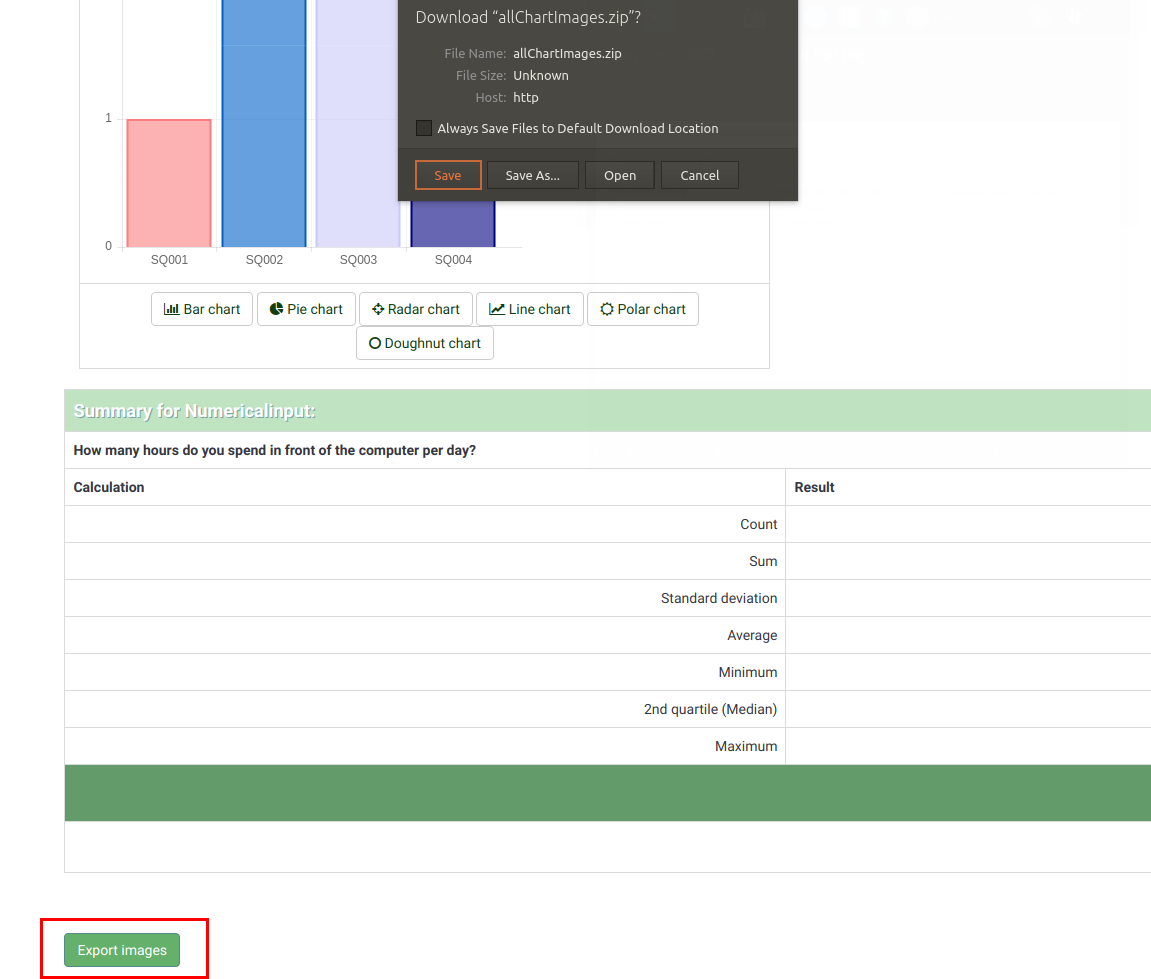
"Incomplete responses", "no answers" and "not completed/not displayed" count
- incomplete responses: All questions started but not completed - the participant clicked the "Next" button in the survey, but did not click the "Submit" button (did not land on the end page of your survey).
There is no SubmitDate in the response table for this entry, but new data set was created already.
- no answer: The question was displayed, but the participant did not an answer.
The question is not mandatory, was displayed, received no answer and the user clicked "Next" or "Submit". The consequence is that the database field for this answer is set to "" (empty string). This "no answer" status cannot be really computed for "Date" or pure "Numerical questions" where the database field cannot record a string.
- not completed/not displayed: The page containing the question was not displayed. This can be because of conditions, or because the participant left the survey before this page was displayed (or while this page is displayed, but without clicking the Next button).
The database field for this question is filled with a NULL value.
Output format and options
The statistics can be displayed in three different formats:
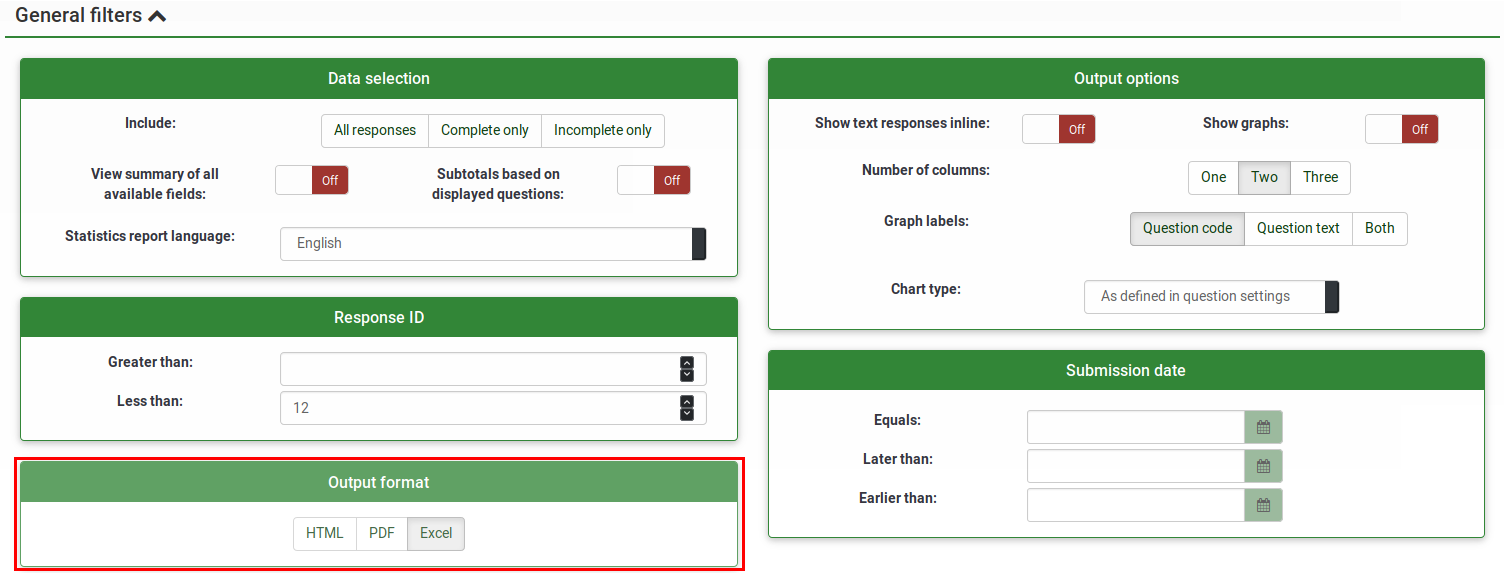
- HTML (default option): The statistics are displayed in LimeSurvey.
- PDF: A popup will be displayed, asking to save the statistics as a PDF file.
- Excel: To further work with your (filtered) data, choose Excel. You can export the file from a spreadsheet application to CSV to work with more advanced statistical tools such as SPSS or R.
The output options can be used to alter the way the statistics are displayed. The following options are available:
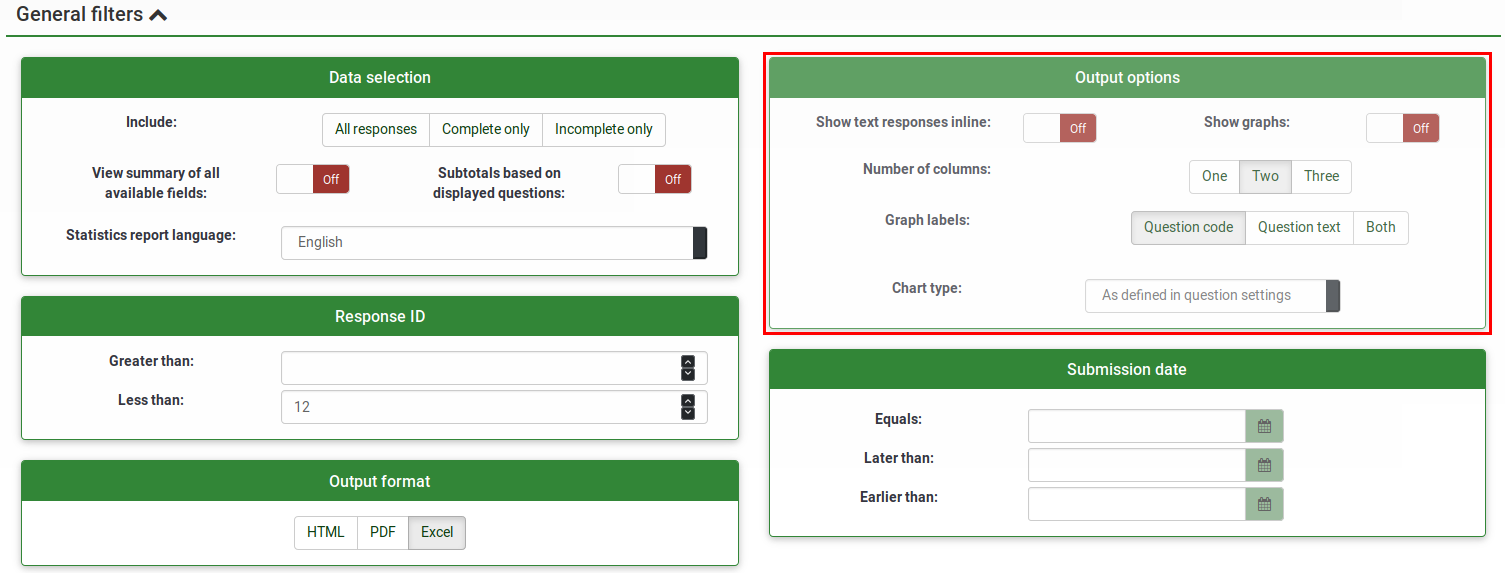
- Show text responses inline: Disabled by default. Shows the text questions responses without having to click a browse button (if enabled; useful for the HTML version of output format)
- Show graphs: Disabled by default. If enabled, graphs will be displayed.
- Number of columns: Two is the default number. If you wish to have statistics and graphs displayed on only one or three columns, choose the desired value from this option. It applies to HTML statistics.
- Graph labels: Choose how the label should look in the graph.
- Question code
- Question text
- Both
- Chart type: the following chart type settings are available:
- As defined in question settings: Useful if you do not want the graph to be displayed. If this is the case, deactivate it from the question settings and select from the "Statistics" panel this option.
- Bar chart
- Pie chart
- Radar chart
- Line chart
- Polar chart
- Doughnut chart
Embed custom logo at statistic PDF
If you want to embed your own logo to the statistics PDF, make sure a file specifically named "statistics.jpg" is placed within the "images" folder of the admin theme used for your system. The admin theme that you would like to use can be set in Global Settings.
Statistics - simple mode
The simple mode was created to provide simple bar chart statistics that can be quickly exported and saved, and then included into a presentation:
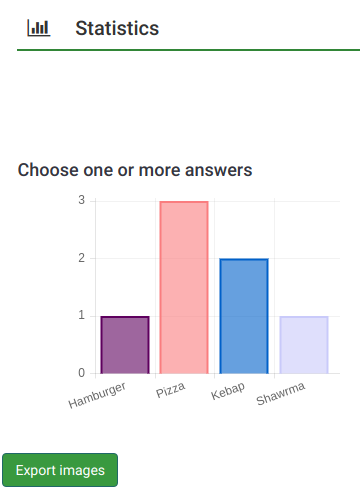
Fewer graphs are displayed than in the expert mode. While in the export mode you can display graphs with respect to those who filled out the survey, did not answer it or did not complete it. the simple mode displays only statistics that rely on the "countable" data submitted by the participants (e.g., single or multiple choice questions as well as array questions).
There is only one option to filter the data within the simple mode - via the responses to be included in the statistics. As a result, the statistics may include the complete responses, incomplete responses, or all responses (the aggregated sum of the first two options). This option is located in the upper-right part of the panel.
To switch back to expert mode, click the "Expert mode" button located in the upper-right part of the screen:

Public statistics
LimeSurvey includes the functionality to display simple statistics to the general public or to your participants after they have completed an online survey.
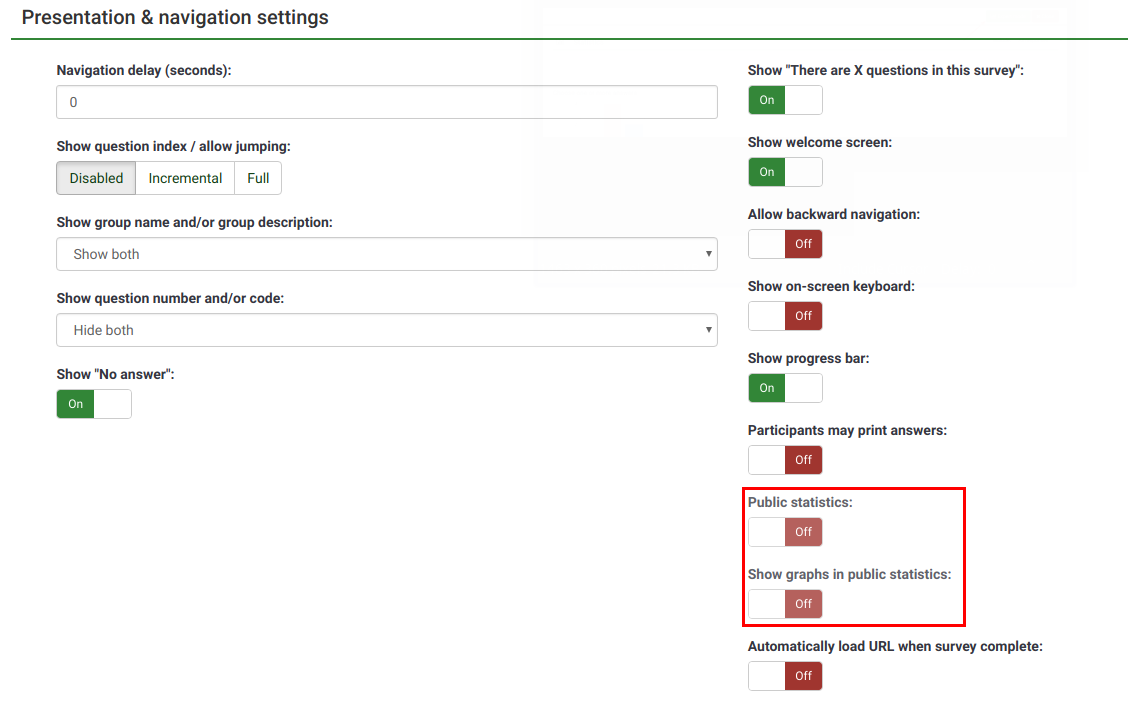
Two components need to be enabled to activate and display statistics to your participants. The first one refers to the public statistics of your survey which must be enabled (it is turned off by default). It is located under the Presentation tab. To also show graphs, look on the same page for the Show graphs in public statistics attribute and enable it (it is disabled by default).
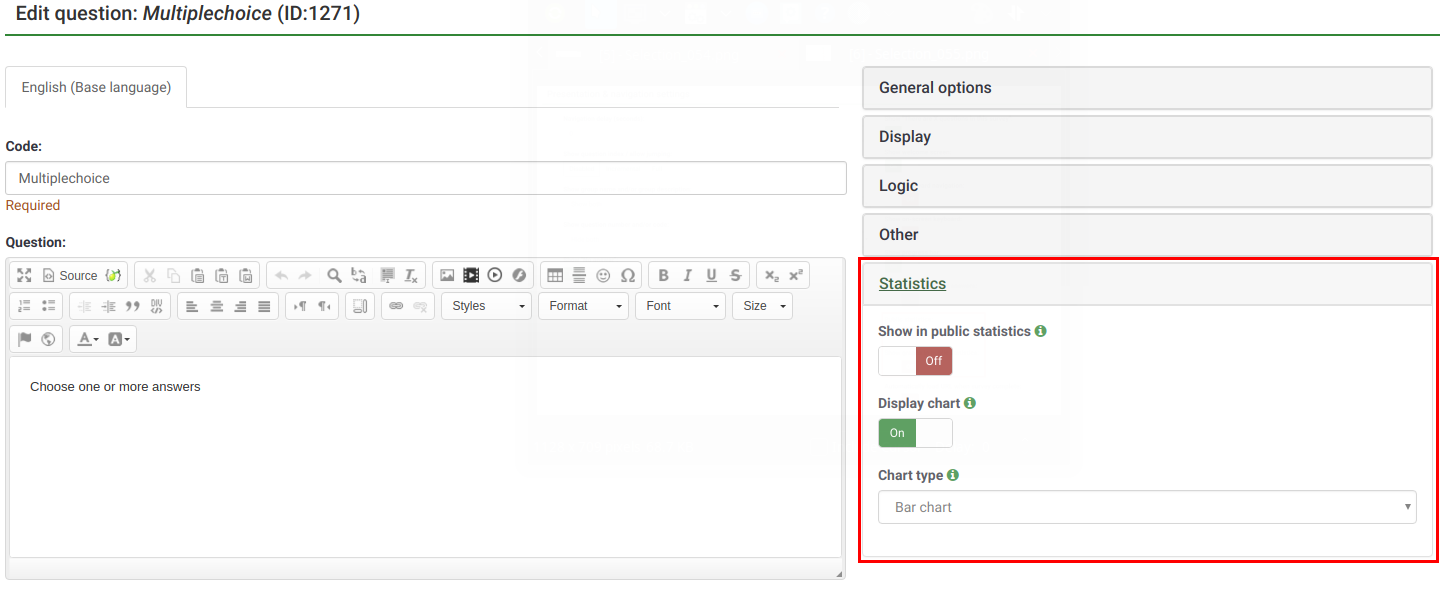
Once you have set your survey to display statistics, you need to indicate question-by-question which statistics you want to be displayed to your respondents. By default, no questions will be displayed. To have them displayed, access the desired question, look for the "Statistics" tab and enable the Show in public statistics attribute.
What participants see
Once you have enabled public statistics and selected some questions to display, an additional option will be visible to participants when they complete your survey. In addition to the usual thank you, there will be a link to "View the statistics for this survey":
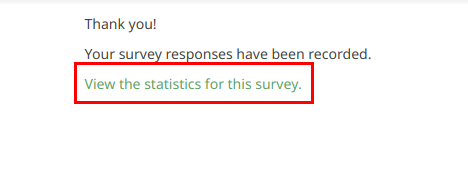
The survey statistics will be displayed on this page. Graphs can also be displayed by enabling the Display chart question attribute:
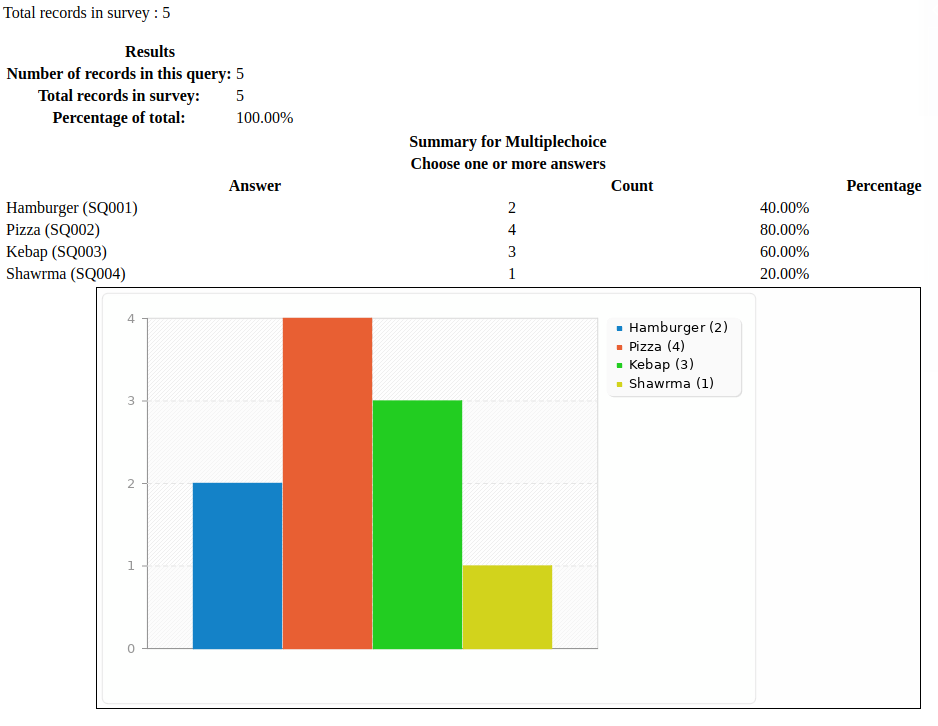
Changing the look of the public statistics page
The apprearance of the public statistics page can be modified via template.css (search for "#statsContainer"). However, there is currently no template on it's own that can be edited in the LimeSurvey theme editor.
Hints & tips
Feel free to edit the following wiki sections to let other LimeSurvey users learn about statistics-related hints & tips.
Wrong font when exporting statistics - what to do?
For some languages (like Chinese), the usual font used (Vera) does not cover the needed character set. In that case you can use the setting $chartfontfile to set a new TTF font file in config.php (Check out config-defaults.php for the right setting). For Chinese (Simplified and Traditional), another font has to be used such as the FireFlySung font which can be downloaded from github.
FAQs
5 Point choice question type - what do the values located under the "sum" column represent?
In the screenshot below, notice that the "Sum" column shows the aggregated values in the following way:
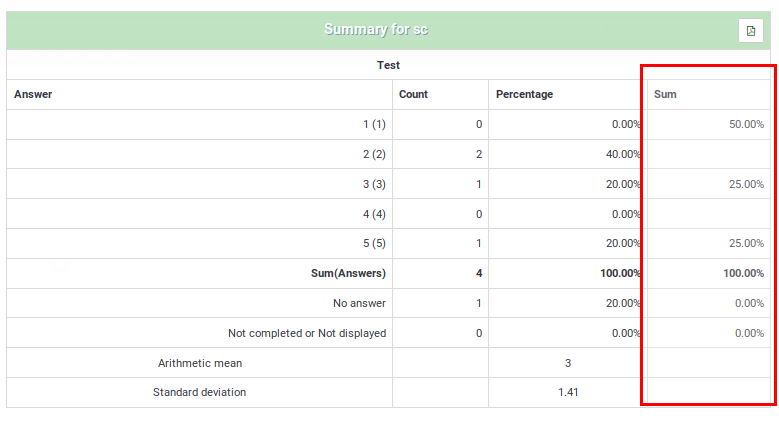
The grouping from the "Sum" column was done in this way because, when rating questions, survey administrators usually interpret the results in this way:
- Y percent of the participants DISLIKE item ABC, where Y represents the percentage of those who answered "1" and "2"
- X percent of the participants LIKE item ABC, where X represents the percentage of those who answered "4" and "5"
- Z percent of the participants have a NEUTRAL opinion about item ABC, where Z represents the percentage of those who answered "3"
| Answer | Count | Sum |
|---|---|---|
| 1 | 0 | 50% (the percentage of those who answered "1" and "2") |
| 2 | 2 | |
| 3 | 1 | 25% (the percentage of those who selected "3" - the neutral option) |
| 4 | 0 | |
| 5 | 1 | 25% (the sum of those who answered "4" and "5") |
| Sum (Answers) | 4 | 100% |
| No answer | 1 | 0% (always "0%") |
| Not completed or displayed | 0 | 0% (always "0%") |